Characteristics of Series Wound DC Generators

In this post, you will learn the characteristics of a series wound dc generator. This article is the continuation of the dc generator characteristics.

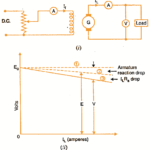
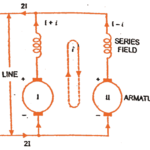
The connection diagram of a series-wound generator is shown in the figure below.

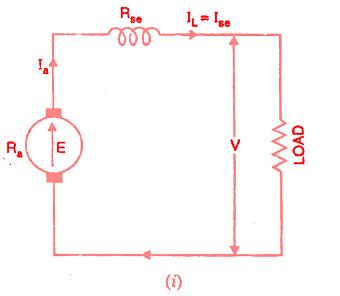
dc series generator connection — Dc series generator connection

Since there is only one current (that which flows through the whole machine), the load current is the same as the exciting current.

The open circuit, internal and external characteristics of series wound dc generators are discussed here.

Open circuit characteristic

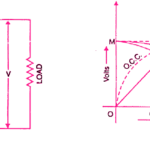
Curve 1 shows the open circuit characteristic (O.C.C.) of a series generator. Curve 2 shows the total or internal characteristics of a series generator. Curve 3 shows the external characteristic of a series generator.

It can be obtained experimentally by disconnecting the field winding from the machine and exciting it from a separate DC source as discussed in dc generator characteristics.

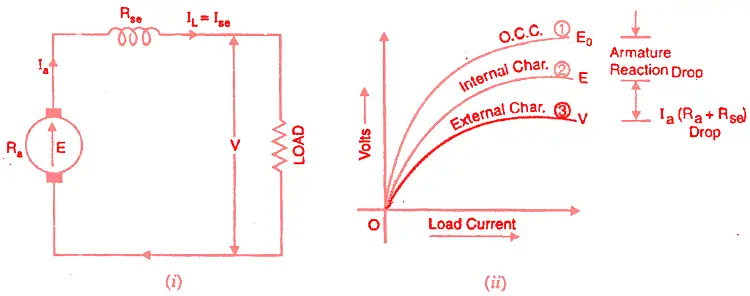
Internal characteristic

Curve 2 shows the total or internal characteristics of a series generator. It gives the relation between the generated e.m.f. E. on load and armature current.

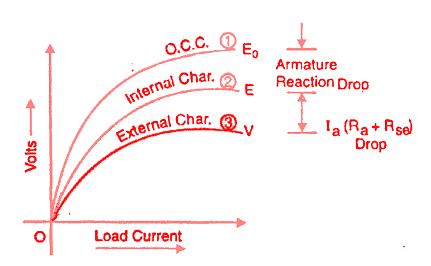
Due to the armature reaction in the dc generator, the flux in the machine will be less than the flux at no load.

Hence, e.m.f. E generated under load conditions will be less than the e.m.f. E0 generated under no-load conditions.

Consequently, the internal characteristic curve lies below the OCC curve; the difference between them representing the effect of armature reaction.

This curve also gives the relation between emf Eg and armature current Ia since Ia=If.

External or Load characteristic

Curve 3 shows the external characteristic of a series generator.

It gives the relation between terminal voltage and load current IL.

V = E – Ia (Ra + Rse )

Therefore, external characteristic curve will lie below internal characteristic curve by an amount equal to ohmic drop [i.e., Ia(Ra + Rse)] in the machine.

This voltage drop for different values of load current may be represented by straight-line OC.

The internal and external characteristics of a dc series generator can be plotted from one another as shown in the figure above.

Suppose we are given the internal characteristic of the generator. Let the line OC represent the resistance of the whole machine i.e. Ra + Rse.

If the load current is OB, drop in the machine is AB i.e. AB = Ohmic drop in the machine = OB(Ra + Rse)

Now raise a perpendicular from point B and mark a point b on this line such that ab = AB. Then point b will lie on the external characteristic of the generator.

Following a similar procedure, other points of the external characteristic can be located.

It is easy to see that we can also plot internal characteristics from the external characteristic. So external characteristic is what we obtain by deducting ohmic drop from internal characteristics.

Note:

From the external characteristic, it is observed that the terminal voltage first increases with the increase in load, reaches the maximum and finally decreases.

If the load resistance is reduced sufficiently, the terminal voltage may fall to zero. So if the series generator is operated on the initial straight-line portion of the characteristic, it gives voltage approximately proportional to the load current.

If it is operated on the drooping portion of the characteristic, it gives approximately constant current irrespective of the external load circuit resistance.